7° Atividade - Aula 8: Map() Dist()

Para essa atividade, precisamos empregar as funções dist() e map() do Processing, explicar e exemplificar como a posição do mouse, numa janela com proporção 4:3, pode mover um círculo no interior de uma retângulo com proporção 16:9 centralizado na tela.

Funcionalidade das funções:

A função dist() é utilizada para calcular a distância entre dois pontos, tanto em 2D, como em 3D. Para cada um dos casos, temos um diferente número de variáveis.

dist(x1, y1, x2, y2):

Esse é o dist() 2D. Nesse caso, o primeiro par é a coordenada (x,y) do primeiro ponto e o segundo par, é a coordenada do segundo ponto.

dist(x1, y1, z1, x2, y2, z2):

Esse é o dist() 3D. Nesse, dois trios de coordenadas, os dois primeiros dois números de cada trio são o mesmo do 2D, já o terceiro, é a posição do ponto no eixo z.

Já a função map(), é utilizada para remapear um valor para alterar um valor para um maior ou menor, mas mantendo a proporção inicial.

Clique para ir para o código

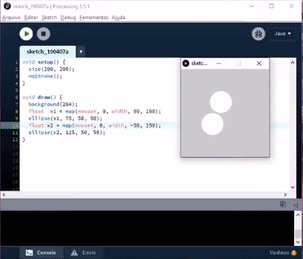
Nesse exemplo, é utilizada uma função map para cada circulo, para definir sua posição no eixo x. A bola de cima pega o valor de mouseX, que vai de 0 a 200 (tamanho da tela) e transforma em um valor que varia de 50 a 150. Já a bola de baixo, pega o mesmo valor de mouseX, e transforma em valores de -50 a 250.

Clique para ir para o código

Conhecendo essas funções, podemos começar o código. primeiramente, vamos definir as proporções. para o retângulo 4:3, vamos usar os valores 800x600. Já para o 16:9, usaremos 480x270.

Agora para a parte principal do código. Primeiramente, vamos de definir o diâmetro do círculo para 10, assim já deixando uma medida padrão.Depois, vamos usar map() para restringir o circulo que representa o mouse ao retângulo menor. Usando as distâncias do da imagem acima, concluímos que o intervalo do retângulo menor no eixo x é de 160 a 640, mas para compensar o tamanho do círculo e não deixar-lo sair da tela, vamos alterar para 165 a 635. Fazendo o mesmo para o eixo y, terminamos com o intervalo 170 a 230, já com a compensação do círculo.

Clique para ir para o código

O resultado final, é o gif acima. Vemos que independente de onde o mouse esteja, o círculo vai estar na posição proporcional.